今回は平方根の計算を学ぶ。 定期テストレベルでは、今回までの内容ができれば、 平方根の分野で平均点以上を取れる。 公立高校入試では、大問1の小問集合などでよく出るので、 確実に得点できるようにしておこう。 前回 ←平方根の計算の準備(基) 次回 →平方根の計算(標)1 平方根 まず、平方の意味はわかりますよね(「2乗する」って意味でしたよね)。 では『平方根』とはいったいなんでしょうか? 『平方根』は「平方」の「根」「根」は根っこ、つまり「もと」という意味ですから、まとめると、 『1 x2=1 x=1 x2=2 x=? x2=4 x=2 x2=5 x=? x2=8 x=? x2=9 x=3 ②④⑤のような場合、あてはまる数が書けないので 2の平方根は と- のように記号を使います x2=a にあてはまる数(解)のことを x の平方根といいます x2=4 のとき x=2とx=-2 なので 4の平方
1の平方根って何ですか 1の平方根は何かと質問されたら答 Yahoo 知恵袋
1の平方根
1の平方根- 中学数学のヤマ場の1つである「平方根 (ルート)」。 しかし、平方根はイメージがしにくい上に、ルートやら計算やら有理化やら、様々な概念が出てくるため理解が難しく、中学生だけでなく高校生でも苦手としている人は多いです。 ですが、高校数学では平方根はわかっていて当然のものとしてほとんどすべての問題に出てきます。 平方根が苦手のまま放っておくこのように01, 01ともに2乗すると001になるので 「001 の平方根は 01 と01 である。




中3 平方根1 中学数学の勉強に
1001 rindas オンラインの平方根計算機を使用して、入力した数値の平方根を見つけます。 平方根 数学では、数値xの平方根は、r 2 = xとなるような数値rです。 例えば、 1 5 2 = 25であるため、25の平方根は5です。 3 2の平方根はおよそです。 3 Piの平方根(π)は約です。 平方根テーブル 以下は、5桁に丸められた1〜1000の平方根テーブルです。平方根基礎1 1 次の数の平方根を求めなさい。(平方根が存在しないときは「ない」と書くこと) ① 4 ② 3 2 ③ 16 ④ –9 ⑤ 121 ⑥ (–7) 2 ⑦ 0 ⑧ x 4 2 次の数の平方根を求めなさい。(ただし、x>0, a>0とする) ① 144 ② 36 ③ 3 ④ 5 ⑤ 1 ⑥ x ⑦ ax ⑧ x 6 ⑨ a 2 x 2 3平方根・累乗根 平方根・累乗根(グラフ) べき乗・累乗 階乗 階乗(グラフ)
平方根(へいほうこん)とは「2乗してaになる数」です。 aを2乗するとa 2 になります。 a 2 はaとaを2乗した数です。 よって、a 2 の平方根は「±a」です。 2乗と平方根は反対の関係だと覚えてください。 また、平方根を表す記号が「√(ルート)」です。 根号ともいいます。 今回は平方根の意味、ルート、求め方、覚え方、公式と問題について説明します。 根号二乗和の平方根を記号で表すと下記です。 c=a 2 b 2 d=√c cの値が二乗和の平方根です。例えば、a=1、b=1とします。cは下記です。 a=2、b=5のとき、cは 2 2 5 2 =29 √29=538 です。 二乗和の平方根の使い方、建築との関係 二乗和の平方根の使い方には POINT 複素数の平方根で有名な1=−1となるパラドックスを紹介. 実数の平方根と異なり,符号を一意に決められないことが原因. 高校生や大学の複素解析を学んだとき,「平方根」で混乱したことはないでしょうか?一見正しそうな計算により,1=−1 が導かれる原因について解説します
1節 平方根 49 2乗するとaになる数を考えよう。 2乗すると9になる数を求めてみましょう。 すなわち,x2= aにあてはまるx の値が の平方根で ある。たとえば,9の平方根は3と-3である。 平方根 次の数の平方根を求めなさい。 ⑴ 16 ⑵ 25 81 ⑴ 2乗すると16になる数は,平方根1 平方根2 循環小数1 循環小数2 平方根の大小1 平方根の大小2 平方根の積と商 ルートの変形1 ルートの変形2 有理化 ルートの乗法除法1 ルートの加法減法1 ルートの加法減法2(変形) ルートの加法減法3(分数) 平方根のおよその値 平方根の四則計算 平方根のいろいろな計算(分配法則) 平方根_式の値 平方根の性質(自然数になる) 平方根の性質(自然数になる2) 有理化2 1 の平方根 =1 2 の平方根 = 3 の平方根




平方根の基本 無料で使える中学学習プリント




中三数学1 6 平方根のまとめ 東華中の過去問から Youtube
平方根(基本) 平方根 根号の変形1 無料で使える中学学習プリント http//chugakumanabihirobanet/ 1 平方根 根号の変形1平方根の計算1 1 次の数の平方根を求めよ。(ただしa>0,b>0,x>0とする) ①49 ②64 ③11 ④x ⑤3 2 ⑥ab ⑦3 ⑧a 2 b 4 ⑨a 8 2 次の数を求めよ。 ① √ 4 ②− √ 25 ③ √ 3 2 ④(√ 7) 2 3 次の計算をしな1 平 方 根 情報の収集 1 平方根(3) 方眼上の正方形の1辺の 長さを調べる活動を通し て「2乗すると2になる 数」などの存在に気付く。 平方根の必要性とその意 味を理解する。 意味,根号を使った表し方などを考えよ 情報の収集 整理・分析 2



平方根まとめ




フラクタル平方根定規 フラクタル自然数1の定義で実現した数学界初の造形 その他雑貨 Art32m Kギャラリ発想力教育研究所 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト
例:若 , = () = = 2的算术平方根 數學史中,最重要的平方根可以說是 ,它代表邊長為1的正方形的對角線長,是第一個公認的無理數,也叫毕达哥拉斯常数,其值到小數點14位約為。 是無理數,可由歸謬法證明: 設 為有理數,可表示為 ,其中 、 為互質之正整數。本词条由 "科普中国"科学百科词条编写与应用工作项目 审核 。 平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为 算术平方根 (arithmetic square root)。 一个正数有两个实平方根,它们 互为相反数 , 负数 没有平方根,0的平方根是0。8 的平方根是什么? 9 的平方根是什么? 10 的平方根是什么? 1 的平方是什么? 11 的平方是什么? 26 的平方是什么? 负数 我们也可以计算负数的平方:




ルートの値を代入する問題 色んな知識を使う良い問題です 中学や高校の数学の計算問題




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
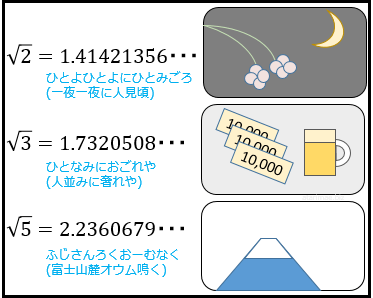
① の平方根は である。 ② ( ) 2 は に等しい。 ③ ± である。 ④ 0の平方根は である。 ⑤ の2乗は である。 ⑥ は の平方根である。 ⑦ 2 である。 ⑧ は である。 3 3 √ 8 8 √ 9 = 3 9 3 5 no1 / 点 6 y 5 = 3 0 √ 36 06 4 16 √6 は √ 動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru2の平方根は、後述するように無理数である。2 の平方根は、人類の歴史において極めて初期の段階で発見されており、おそらく最初に知られた無理数であると考えられている。幾何学的には、1辺の長さが 1 の正方形の対角線の長さに相当する。



3 25第2章1平方根 平方根とは 中学生



Http Www Naka H Ibk Ed Jp Action Common Download Main Upload Id 2375
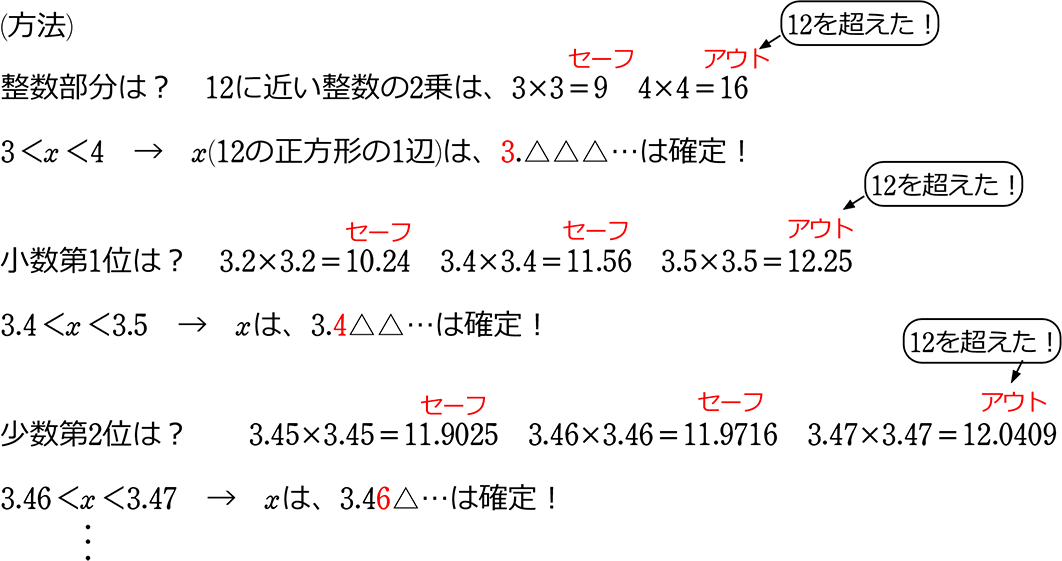
平方根計算法 実行結果 正整数 12の平方根の整数部 = 3 正整数 1234の平方根の整数部 = 35 正整数 の平方根の整数部 = 351 正整数 の平方根の整数部 = 3513 ok 改良 1234の平方根を求める。 1234を2桁ずつに分ける。 ①12の平方根を求める。 0 < 12 135 < 12 < 1357平方根1_平方根を求める x 2 =A のとき xをAの 平方根 という。 正の数には平方根が2つ,0の平方根は0だけで,負の数には平方根はない, 解説動画 ≫ 次の数の平方根を求めよ。平方根 へいほうこん square root 実数 a に対して,x 2 =a を満たす実数 x を a の平方根と呼ぶ。 a が正数のとき a の平方根は正数であるものと負数であるものの二つが存在し,このうち正の方を√a で表す。 0の平方根は 0である。たとえば,√2=,√3=であり,これらは




中学数学 平方根のひみつ 都立高校入試で成功する方法




平方根の加減 チーム エン
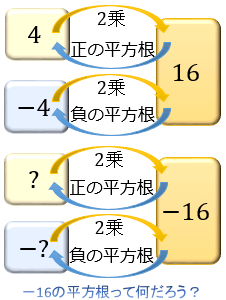
61平方根第一节 48播放 105弹幕 正在缓冲 播放器初始化 加载视频内容 65 22 43 36 动态 微博 QQ QQ空间 贴吧 将视频贴到博客或论坛 视频地址 复制基本的に平方根は、このように+と-の数がセットで出てきます。 なので、これらをまとめて と表していくようになります。 (これをプラスマイナス2と読みます) それでは、例題をいくつか 9の平方根は ⇒ 25の平方根は ⇒ 81の平方根は ⇒ 平方根は① の平方根は である。 ② ( ) 2 は に等しい。 ③ ± である。 ④ 0の平方根は である。 ⑤ の2乗は である。 ⑥ は の平方根である。 ⑦ 2 である。 ⑧ は である。 no2 / 点 7 7 y = 3 16 4 √ 5 5 √81 = 9 0 √7 7 11 121 √13 は 13 √ 09 03




平方根とは 中学数学 平方根 1 Youtube




世界一わかりやすい数学問題集中3 2章 平方根
定义:在分数指数中,依定义,可知开平方运算对乘法满足分配律,即:注意若n是非负实数且时,因为必定是正数,但有正负两个解。 应等于±;即 (见绝对值)。 图1平方根 若一个数x,它的的平方等于a,即 x²=a, 若x的平方等于a,那么x就叫做a的平方根,即√a ̄=x 像加减乘除一样,求平方根也有自己的竖式运算。 以求3的算术平方根为例,过程如图1:解得3的算术平方根 id 分类: 课件 , 知识点 , 全国 , 21 资源大小:955kb 资料长标题:31平方根同步课件 2122学年浙教版数学七年级上册 资料简介 第三章 实数 31 平方根 知识回顾 32 =( ) ( 3 )2=( ) ( ±3 )2=( ) 9 9 9 获取新知 一张正方形桌面的面积为144m2, 它的边长为多少米?他の例として四元数体 H において、 −1 は ±i, ±j, ±k を含む無数の平方根を持つ。実は −1 の平方根の全体はちょうど集合 { =} であり、したがって各平方根は絶対値が等しく、この集合は三次元空間内の二次元単位球面を描く。四元数#−1 の平方根も参照。 零元 0 の平方根は、定義により、 0 自身または零因子である。




平方根の式の値 無料で使える中学学習プリント




平方根とは何 Weblio辞書
平方根(基本) 平方根11 無料で使える中学学習プリント http//chugakumanabihirobanet/ 1 平方根1 名前 1.2乗すると,次の数につまり1の平方根は±1 (□) 2 = 9のとき □には3, または3がはいるので、9の平方根は±3 このように 正の数の平方根は、正と負の2つあり、それらの絶対値は等しい。 1到10的平方根分别是多少: 1的是12的是的是的是25的是的是的是的是的是310的是 一至十的平方根精确到001: 平方根,又叫二次方根,表示为〔√ ̄〕,其中属于非负数的平方根称之为算术平方根一个正



1



平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ
平方根のポイントは!・平方根とは「 2 乗の根っこ」のことで、プラスとマイナスの 2 個存在する!・ 0 の平方根は 0 のみ!




平方根はなぜプラスとマイナス両方あるの ルートの基本を確認 あんず学習塾のメモ 図表置き場




中3 平方根1 中学数学の勉強に




平方根の利用 1 整数 自然数になるようなn 標 難 数学の解説と練習問題




1 2乗って何 どうしてそれがルート 平方根 になるのか 数学の面白いこと 役に立つことをまとめたサイト




平方根の問題の解き方 6パターン 数学fun




Tossランド 平方根 の暗記プリント Dl可




5分動画 1の立方根 4乗根 5乗根 6乗根 数学ii 複素数と方程式 Youtube




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




数1の平方根と式の値です Clear



平方根の覚え方 中学から数学だいすき




平方根の問題の解き方 6パターン 数学fun




平方根 1 基本のルール バカでもわかる 中学数学




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




フラクタル平方根定規 フラクタル自然数1の定義で実現した数学界初の造形 その他雑貨 Art32m Kギャラリ発想力教育研究所 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト




数学 平方根を含む式の計算のやり方とコツ 教科書より詳しい高校数学




2次方程式 1 解き方 因数分解 平方根 平方完成 解の公式 バカでもわかる 中学数学




ม 3 โน ตของ 中3 2章 平方根 1節 平方根 ช น Junior Clear



中学数学 平方根




中学校 3年 数学 平方根を小数で表した時の小数第1位の数の 求め方を 数学 教えて Goo




2の平方根 Wikipedia




無料 中3数学 基本解説 解答プリント 309 平方根1 意味




数学i 1次不等式 2 1 平方根 Youtube




平方根 ルート0 1と0 1はどちらが大きい 中学数学 定期テスト対策サイト




中学数学の勉強に 5ページ目




2の平方根 Wikipedia
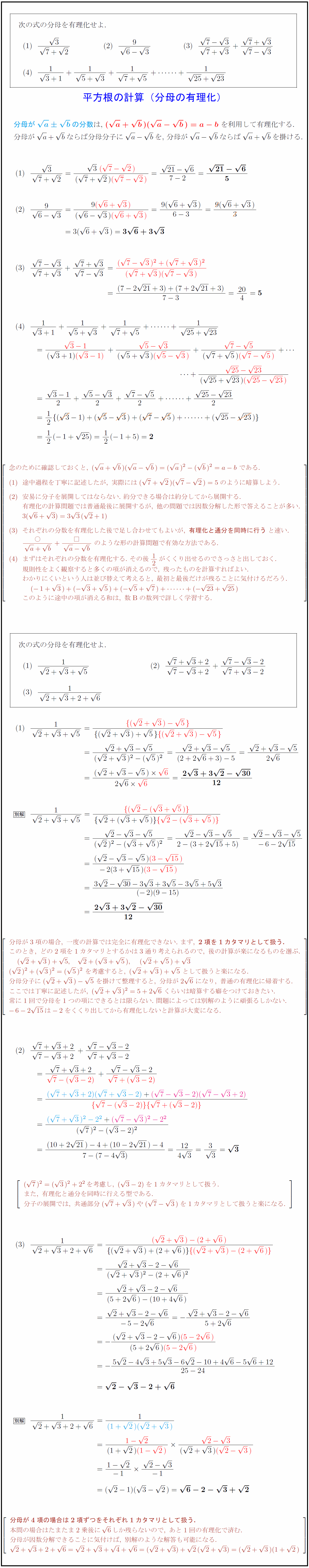



高校数学 平方根の計算 分母の有理化 受験の月




1 1 の は 5の平方根は 5 なのに なぜ2 の 2 Clear




平方根の応用 無料で使える中学学習プリント




ポテト一郎 平方根パズルを考えました 解けたらrt



中学数学 平方根




数と式 平方根について 日々是鍛錬 ひびこれたんれん




平方根 数学の要点まとめ 練習問題一覧




中学校数学 3年生 数量 平方根 Wikibooks




数学の一問一答 平方根 勿忘荘




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




平方根 2 ルートと平方根の違い バカでもわかる 中学数学



Www Pref Oita Jp Uploaded Attachment Pdf




複素数の平方根1 定義と高校数学の両面から考える 身勝手な主張




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ



1
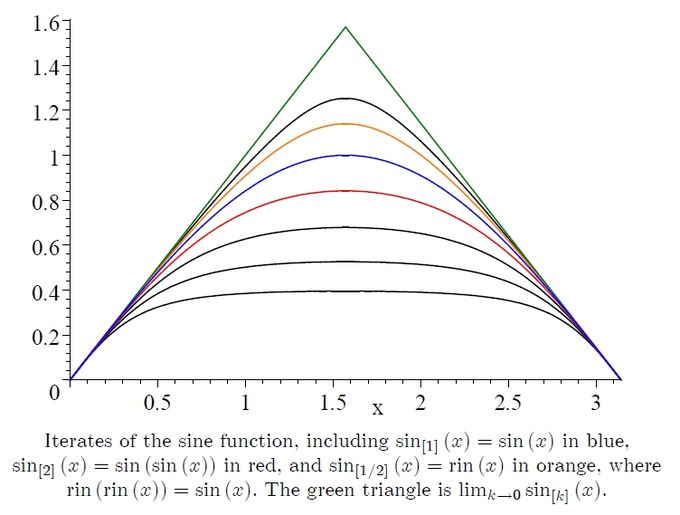



函数的平方根 Wikipedia



1の平方根って何ですか 1の平方根は何かと質問されたら答 Yahoo 知恵袋




平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師
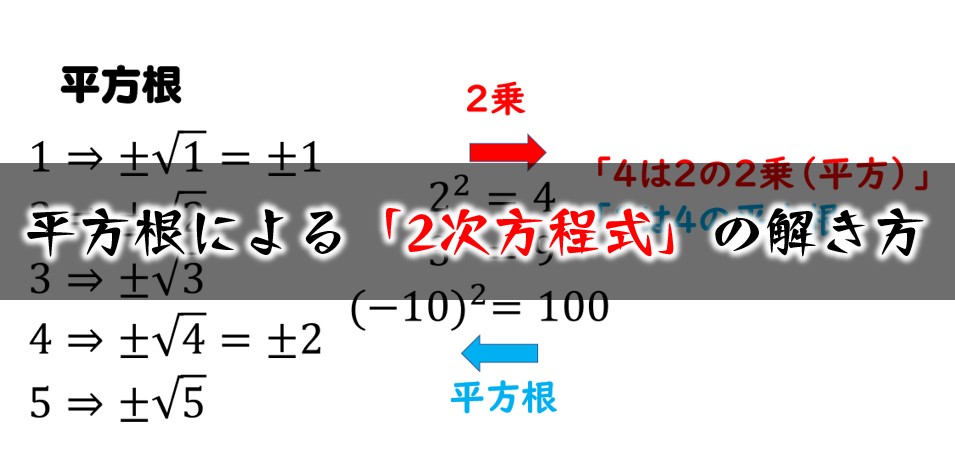



2次方程式の解き方 平方根を利用 数学fun



次の数の平方根を求めよ教えてください 16と49と9分の1と10やり Yahoo 知恵袋




1 2乗って何 どうしてそれがルート 平方根 になるのか 数学の面白いこと 役に立つことをまとめたサイト



2乗 平方根




高認数学 第1回 式の計算



中学3年 平方根 第1講 清水塾



1 9の平方根を教えてください 49分の1の平方根を教えてください 数 Yahoo 知恵袋




中学数学 平方根の利用 ママ塾ノート
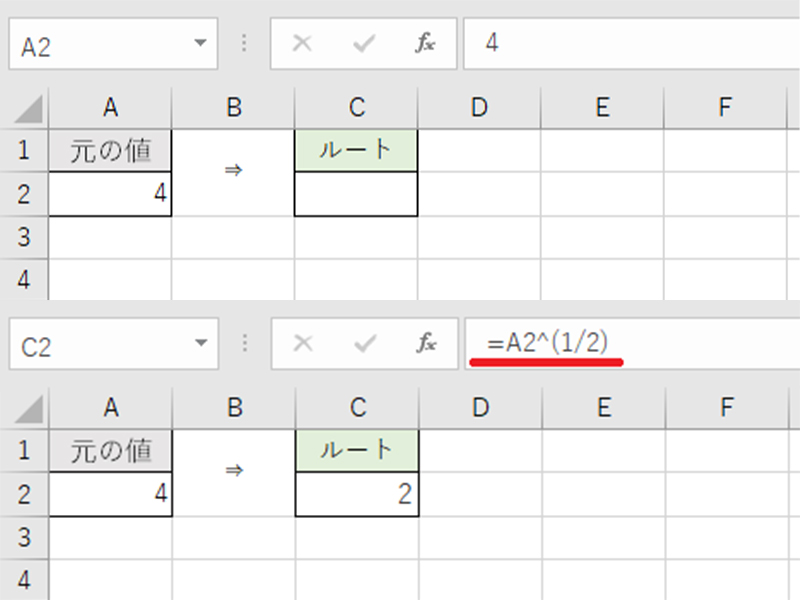



画像あり エクセルの関数を使ってルート 平方根 を計算 表示するには 基本と応用 ワカルニ




Tossランド 平方根の授業 3時間目 1




平方根とは コトバンク




世界一わかりやすい数学問題集中3 2章 平方根



Www Pref Gifu Lg Jp Uploaded Attachment Pdf




平方根 とは 根号の意味や性質 値の求め方について 数学fun



1



フナハシ学習塾数学03 計算 ルート平方根




マイナス1の平方根 エナジーフラワーエッセンス療法 アクセスバーズ バッチフラワーオラクルカード 横浜青葉区おうちサロンモーニングデュウ



1の平方根って何ですか 1の平方根は何かと質問されたら答 Yahoo 知恵袋



高1数学平方根と式の値の問題です 問題は画像の通りです 解き方がわからな Yahoo 知恵袋



平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ



Studydoctor根号 ルートと式の値 中3数学 Studydoctor




平方根の計算 やり方は をつけてルートをつけよう 中学や高校の数学の計算問題




数と式 平方根について 日々是鍛錬 ひびこれたんれん



3




勝手に北辰テスト対策 数学 平方根 蒼進塾 そうしんじゅく さいたま市 真剣に努力する姿勢を育む




Amazon Co Jp 数学が苦手な人におススメ 中1でもわかる高校数学 平方根編 中3と高1で学習する平方根が中1でもラクラクわかる Ebook ぴょん インオミ 本




フラクタル平方根定規 フラクタル自然数1の定義で実現した数学界初の造形 その他雑貨 Art32m Kギャラリ発想力教育研究所 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト



平方根の筆算のしかた



中3数学 平方根の性質の定期テスト対策問題 Examee




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ



超簡単 平方根の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




ルート 平方根 二乗根 計算機 かんたん計算機




中学3年生 数学 平方根の加法 減法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平方根とルート 根号 の概念 有理数と無理数の違い リョースケ大学




中学3年生 数学 平方根 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中学数学 平方根



1的平方根是1对不对 初三网
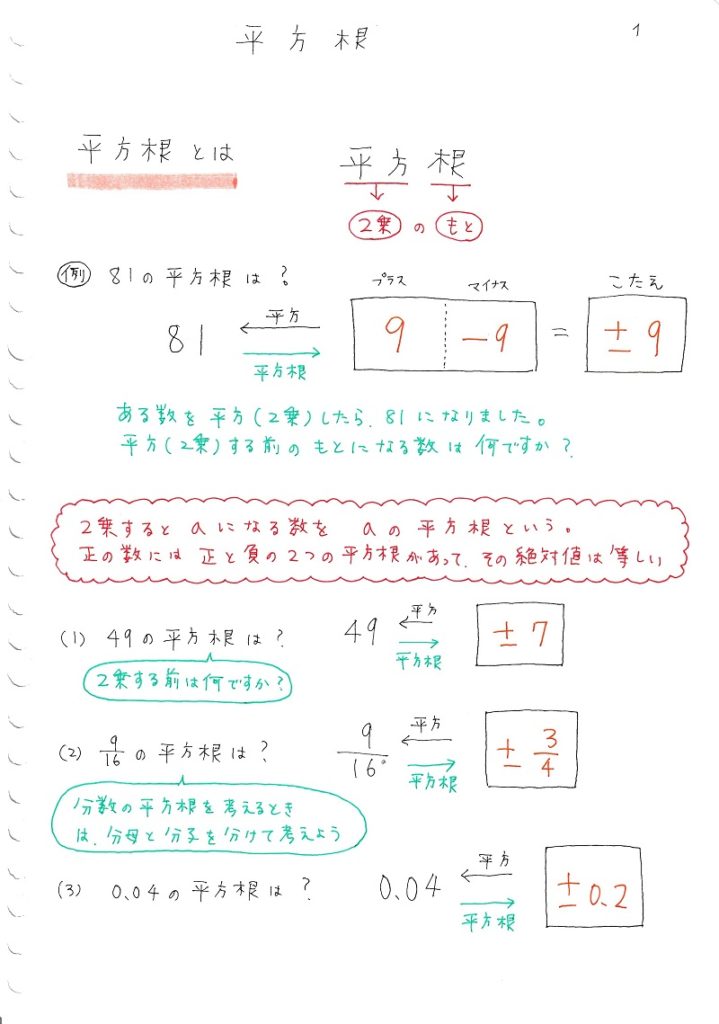



中学数学 平方根 ママ塾ノート




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月




数学問題集の部屋 平方根の計算 入試問題1の解答




中3 平方根 中学生 数学のノート Clear




平方根の求め方って 分数や小数の時はどうしたら良いの さびねこ中学校



2




中学3年 数学 東京書籍 2章1節 平方根 解答 解説 赤城 ᐡᐤᐡ




平方根の大小 無料で使える中学学習プリント



0 件のコメント:
コメントを投稿